Plan semanal

1. Reducción al absurdo
2. Contra la multiplicidad
3. Contra el movimiento
4. La defensa del movimiento

Reducción al absurdo

¿Cuántos números primos hay?

Supongamos que solo hay una cantidad finita de números primos. De ser así, podemos ponerlos todos en una lista grande, y multiplicarlos a todos. Llamamos N al resultado. Pero entonces el número n+1 no es múltiplo de ninguno de los primos en la lista, lo que significa que o es un número primo, o es un producto de primos que no están en la lista. En cualquier caso se llega a una contradicción, pues o bien N es un primo que no está en la lista o es producto de números primos que no están en la lista. En cualquiera de los dos casos, habría números primos que no están en la lista. Luego, la suposición inicial no es correcta.

• Supongamos que sólo hay una cantidad finita de números primos
• Si hay una cantidad finita de primos, entonces se les puede escribir en una lista
• Llamar 'N' al resultado de la multiplicación de todos los números en la lista
• Llamar 'M' al resultado de sumar 1 a N
• O bien M es múltiplo de primos en la lista, o bien múltiplo de primos que no están en la lista, o bien es un número primo.
• M no es múltiplo de los números primos en la lista
• O bien M es múltipo de números primos que no están en la lista o bien es un número primo
• Si M es múltiplo de primos que no están en la lista, entonces hay numeros primos que no están en la lista
• Si M es un número primo, entonces hay un número primo que no está en la lista.
• Entonces no se puede escribir una lista con todos los primos
• Entonces la suposición de que los números primos son finitos es incorrecta.

¿El profesor es hincha de Millonarios o de Santa Fé?

Supongamos que el profe es de Santa fé. Si eso fuese así, entonces tendría una camiseta oficial, iría al estadio, seguiría los partidos y otras manifestaciones propias de un hincha. El profe no hace nada de eso. Luego, la suposición es incorrecta y el profe es de Millonarios.

¿Qué opinan de estas premisas implícitas?

Contra la multiplicidad

"Si existe la multiplicidad, ésta estará integrada por unidades que o poseen magnitud o no poseen magnitud. Si poseen magnitud, entonces cada unidad constará de partes, relacionadas unas con otras, y nunca podrá decirse que una parte sea la última, por consiguiente estas partes serán infinitas y la multiplicidad que ellas integren será infinitamente grande. Si las unidades no poseen magnitud, cada unidad no altera aquello a lo cual se agrega o de lo cual se quita; entonces no posee realidad alguna y la multiplicidad integrada por estas partes será infinitamente pequeña. La aporía de la multiplicidad consiste así, en que si la multiplicidad existe, ella será tanto infinitamente grande como infinitamente pequeña." (Campos: 27)

1. Si existe la multiplicidad, ésta estará integrada por unidades que o poseen magnitud o no poseen magnitud
2. Si las unidades poseen magnitud, entonces cada unidad constará de partes, relacionadas unas con otras, y nunca podrá decirse que una parte sea la última, por consiguiente estas partes serán infinitas y la multiplicidad que ellas integren será infinitamente grande.
3. Si las unidades no poseen magnitud, cada unidad no altera aquello a lo cual se agrega o de lo cual se quita; entonces no poseen realidad alguna y la multiplicidad integrada por estas partes será infinitamente pequeña.
4. La aporía de la multiplicidad consiste así, en que si la multiplicidad existe, ella será tanto infinitamente grande como infinitamente pequeña.

Descompongan el argumento en premisas y conclusión simples —así como hicimos con el argumento para mostrar que los números primos no son finitos

¿Están de acuerdo con el argumento?

1. Si existe la multiplicidad, ésta estará integrada por unidades que o poseen magnitud o no poseen magnitud
2. Si las unidades poseen magnitud, entonces cada unidad constará de partes, relacionadas unas con otras, y nunca podrá decirse que una parte sea la última, por consiguiente estas partes serán infinitas y la multiplicidad que ellas integren será infinitamente grande.
3. Si las unidades no poseen magnitud, cada unidad no altera aquello a lo cual se agrega o de lo cual se quita; entonces no poseen realidad alguna y la multiplicidad integrada por estas partes será infinitamente pequeña.
4. La aporía de la multiplicidad consiste así, en que si la multiplicidad existe, ella será tanto infinitamente grande como infinitamente pequeña.

Contra el movimiento

pues a cualquier número se le puede sumar 1
y tener un número más grande

pues no hay forma de ofrecer una caracterización
no circular de la noción.

pues si lo hubiese no habría maldad en el mundo

pues ...

Tres aporías

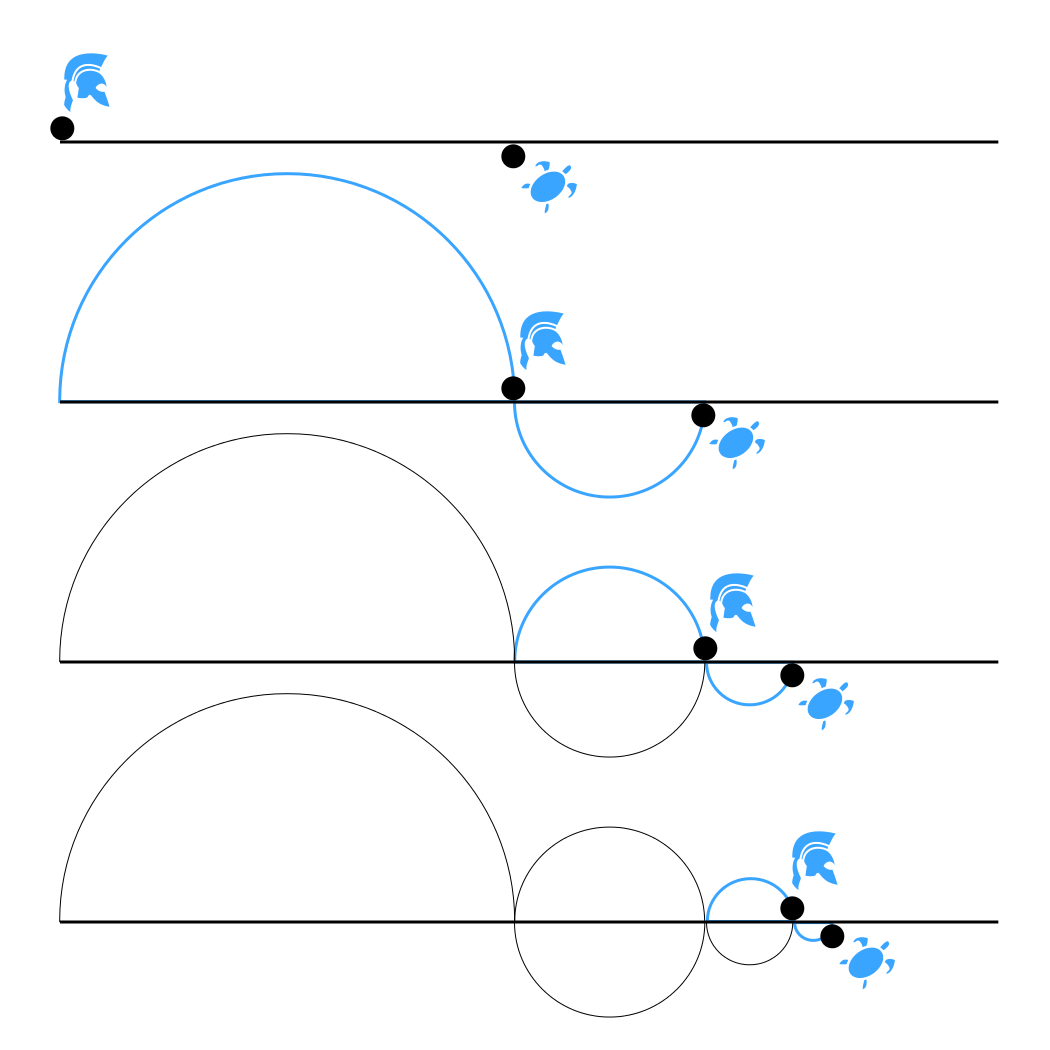
Aquiles y la tortuga

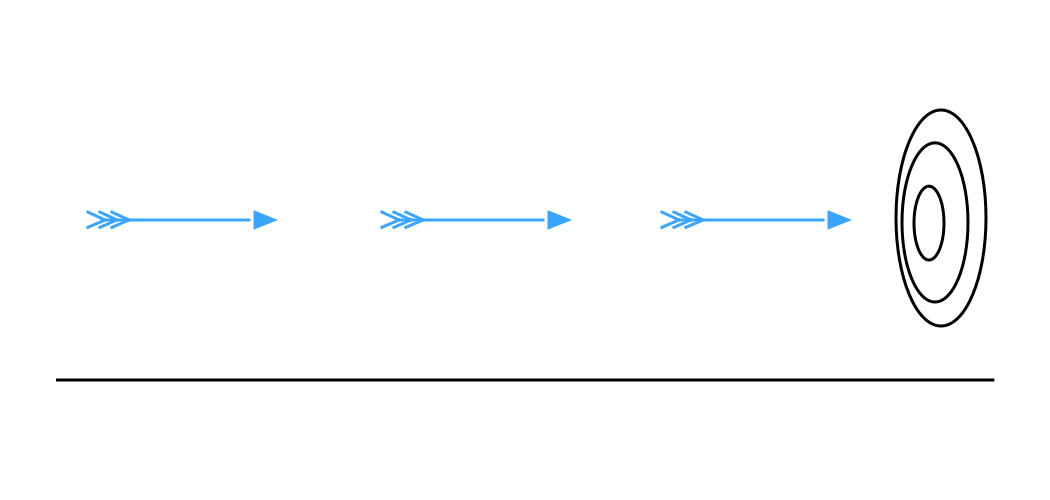
La flecha

Dictomía

Una versión moderna de las paradojas del espacio

1. Si el transporte en transmilenio es posible, entonces es posible ir de una estación A a una estación Z.
2. Para ir de la estación A a la Z es necesario hacer trasbordo en la estación Y
3. Para ir de la estación A a la Y es necesario hacer trasbordo en la estación X
4. Para ir de la estación A a la X es necesario hacer trasbordo en la estación W
5. Para ir de la estación A a la W es necesario hacer trasbordo en la estación V
6. Y así infinitamente
7. No es posible hacer infinitos trasbordos
8. El transporte en transmilenio no es posible

1. Si el movimiento es posible, entonces es posible ir de un punto A a una punto Z.
2. Para ir del punto A a la Z es necesario ir al punto Y
3. Para ir del punto A a la Y es necesario ir al punto X
4. Para ir del punto A a la X es necesario ir al punto W
5. Para ir del punto A a la W es necesario ir al punto V
6. Y así infinitamente
7. No es posible dar infinitos pasos
8. El movimiento no es posible

Una versión moderna de las paradojas del tiempo

1. En las películas se da la apariencia de movimiento
2. En las películas hay 24 fotogramas por segundo.
3. Entre fotograma 1 y fotograma 2 no hay movimiento. Son dos imágenes estáticas.
4. Entre fotograma 2 y fotograma 3 no hay movimiento. Son dos imágenes estáticas.
5. Entre fotograma 3 y fotograma 4 no hay movimiento. Son dos imágenes estáticas.
6. Entre fotograma 4 y fotograma 5 no hay movimiento. Son dos imágenes estáticas.
7. Así para todos los casos.
8. En las películas no hay movimiento. Es mera apariencia.

1. En las mundo real hay la apariencia de movimiento
2. El movimiento se da entre un instante A y un B
3. En un instante, no hay movimiento pues el movimiento es en el tiempo.
4. En los instantes A y B no hay movimiento, pues son instantes.
5. Entre los instantes A y B no hay nada.
6. A fortiori, entre los instantes A y B no hay movimiento
7. En el mundo real no hay movimiento. Es mera apariencia; es una película a 60 fotogramas por segundo.

La defensa del movimiento

¿Cuál es el problema de esta respuesta?

¿Cuál es la diferencia entre el infinito actual y el potencial?

Para la próxima clase

• Campos, Alberto (1994) Axiomática Y Geometría Desde Euclides Hasta Hilbert Y Bourbaki. Bogotá, Colombia: Universidad Nacional. Cap. Euclides (★)